4/4 월

월요일!

 

오늘은 금요일에 실습 예제로 주어졌던 admission(대학원 합격 여부) 데이터셋을 Sklearn, Tensorflow로 구현하고,

지난주에 배운 Logistic Regression을 활용해 평가지표(Metrics)를 알아본다.

 

1. Logistic Regression by Sklearn

import numpy as np
import pandas as pd
import tensorflow as tf
from sklearn import linear_model
from sklearn.preprocessing import MinMaxScaler
from scipy import stats
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')

df = pd.read_csv('./data/admission.csv')

# display(df.head())
# df.info()
# print(df.isnull().sum()) # 결치값 없음

# figure = plt.figure()
# ax1 = figure.add_subplot(1,4,1)
# ax2 = figure.add_subplot(1,4,2)
# ax3 = figure.add_subplot(1,4,3)
# ax4 = figure.add_subplot(1,4,4)

# ax1.set_title('ADMIT')
# ax2.set_title('GRE')
# ax3.set_title('GPA')
# ax4.set_title('RANK')

# ax1.boxplot(df['admit'])
# ax2.boxplot(df['gre'])
# ax3.boxplot(df['gpa'])
# ax4.boxplot(df['rank'])

# figure.tight_layout()
# plt.show() # df['gre'], df['gpa']에 이상치가 있다

zscore_threshold = 2.0 # zscore로 이상치 제거
for col in df.columns:
    outlier = df[col][np.abs(stats.zscore(df[col])) > zscore_threshold]
    df = df.loc[~df[col].isin(outlier)] # ~는 Not

x_data = df.drop('admit', axis = 1, inplace=False) # 정규화 진행
t_data = df['admit'].values.reshape(-1,1) # 0과 1로만 구성되어 있음

scaler = MinMaxScaler()
scaler.fit(x_data) # fit으로 변환을 위한 사전구조 맞추기

norm_x_data = scaler.transform(x_data) # 0 ~ 1 사이의 값으로 변환
# print(norm_x_data) # norm_x_data, t_data 준비

model = linear_model.LogisticRegression() # Sklearn 구현
model.fit(x_data, t_data)
my_score = np.array([[600, 3.8, 1]])
predict_val = model.predict(my_score) # 1. 0 or 1로 결과 도출
predict_proba = model.predict_proba(my_score) # [[0.43740782 0.56259218]]. 확률값으로 결과 도출

print('Sklearn이 예측한 결과 : 합격여부 : {}, 확률 : {}'.format(predict_val, predict_proba)) # 합격!

 

2. Logistic Regression by Tensorflow

X = tf.placeholder(shape=[None,3], dtype=tf.float32) # placeholder
T = tf.placeholder(shape=[None,1], dtype=tf.float32)

# Weight, bias
W = tf.Variable(tf.random.normal([3,1]))
b = tf.Variable(tf.random.normal([1]))

# Hypothesis, Model, Predict Model, Logistic Regression Model
logit = tf.matmul(X,W) + b
H = tf.sigmoid(logit)

# loss func, cross entropy 혹은 log loss
loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=logit, labels=T)) # logits은 선형회귀, y. label은 T

# train node
train = tf.train.GradientDescentOptimizer(learning_rate=1e-4).minimize(loss)

# Session & 초기화
sess = tf.Session()
sess.run(tf.global_variables_initializer())

# 반복 학습
for step in range(300000):
    _, loss_val = sess.run([train, loss], feed_dict={X: norm_x_data, T: t_data})
    
    if step % 30000 == 0:
        print('loss의 값 : {}'.format(loss_val))

# Prediction + MinMaxScaler
my_score = np.array([[600, 3.8, 1]])
norm_my_score = scaler.transform(my_score)

result = sess.run(H, feed_dict={X: norm_my_score})
print('Tensorflow가 예측한 : 확률 : {}'.format(result)) # [[0.4715909]]. 불합격!

 

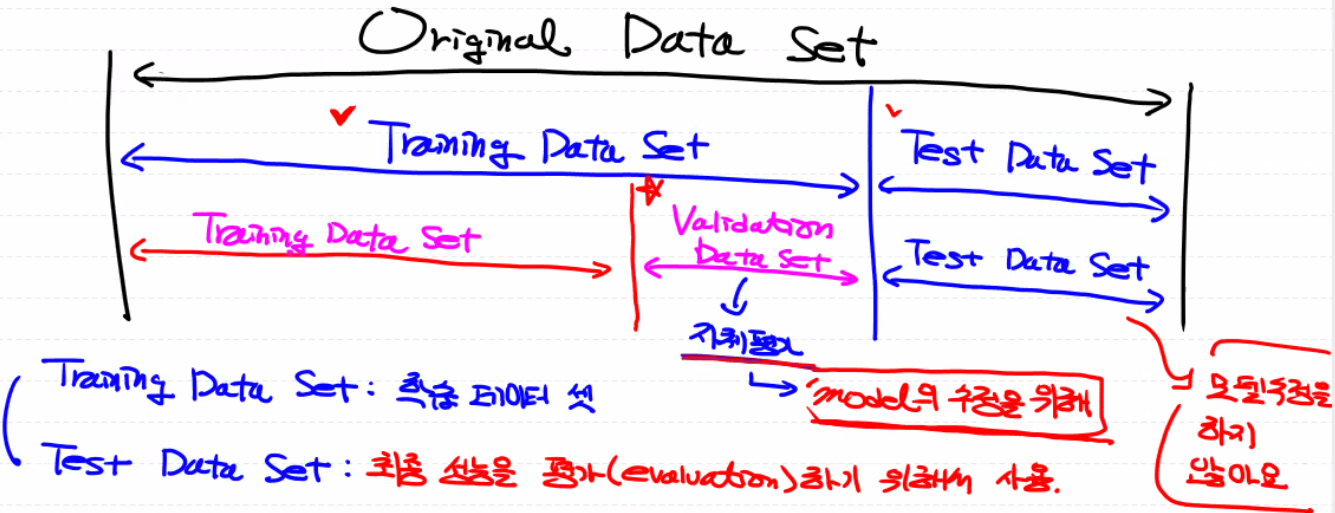
Model을 구현한 후 Evaluation(성능평가)를 진행해야 함 - Metrics

 

Training Data Set을 이용해서 학습한 뒤, Training Data Set을 이용해서 성능평가를 하면 당연히 안됨!

(모의고사 문제 = 본고사 문제)

 

그러므로, Original Data Set을 Training(독립 · 종속변수 혼재)과 Test Data Set(독립변수만)으로 나눠줘야 함

예측을 제출하기 전 자체 평가하기 위해, Training Data Set을 Validation Data Set으로 또 나눠줌(Model의 수정)→ Hold-Out Validation : Training Data Set의 일부를 Validation Data Set으로 희생단점 : 데이터 양이 적으면 쓰기 곤란함, 데이터의 편향이 생길 수 있음

 

다른 Validation 방식은 K-Fold Cross Validation 

 

1. Regression의 Metrics (Hold-Out Validation, Sklearn)

import numpy as np
import pandas as pd
from sklearn import linear_model
from scipy import stats
from sklearn.model_selection import train_test_split # Training set / Test set 나누기

df = pd.read_csv('./data/ozone.csv')
# print(df.shape) # (153, 6)

training_data = df.dropna(how='any', inplace=False) # 결측치 제거
# print(training_data.shape) # (111, 6)

zscore_threshold = 2.0 # zscore로 이상치 제거

for col in training_data.columns:
    outlier = training_data[col][np.abs(stats.zscore(training_data[col])) > zscore_threshold]
    training_data = training_data.loc[~training_data[col].isin(outlier)] # ~는 Not

# display(training_data.head()) # Sklearn 쓸 거라서 정규화는 따로 하지 않음

# Data Set
x_data = training_data[['Solar.R', 'Wind', 'Temp']].values
t_data = training_data[['Ozone']].values.reshape(-1,1)

# Train / Validation Data Set으로 분리
train_x_data, valid_x_data, train_t_data, valid_t_data = \
train_test_split(x_data,
                 t_data,
                 test_size=0.3,
                 random_state=2) # random_state은 seed 역할

# print(train_x_data.shape, valid_x_data.shape, train_t_data.shape, valid_t_data.shape)
# (67, 3) (29, 3) (67, 1) (29, 1)

# Model
model = linear_model.LinearRegression()

# Model 학습
model.fit(train_x_data, train_t_data)

# 예측값. 정답은 valid_t_data
predict_value = model.predict(valid_x_data)

- 1. MAE(Mean Absolute Error) : 예측값과 정답의 차이를 절대값으로 평균 냄

직관적이고 단위가 같으나 scale(종속변수의 단위)에 따라 의존적임

from sklearn.metrics import mean_absolute_error # MAE

print(mean_absolute_error(valid_t_data, predict_value)) # 13.924465776324642

- 2. MSE(Mean Squared Error) : 오차의 제곱의 평균. MAE보다 이상치에 민감함

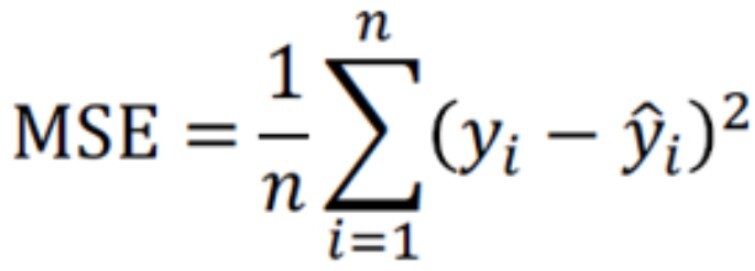
from sklearn.metrics import mean_squared_error # MSE

print(mean_squared_error(valid_t_data, predict_value)) # 271.5671192367061

- 3. RMSE(Root Mean Squared Error) : MSE에 루트 씌운 것

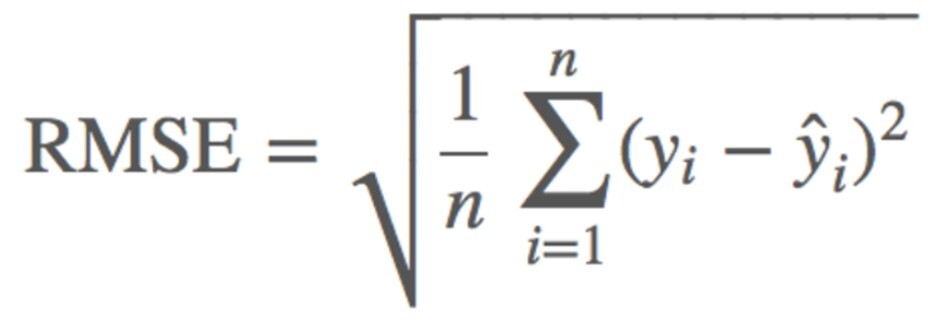
- 4. MAPE(Mean Absolute Percentage Error) : MAE의 100 분율 표현. 값이 작을수록 좋은 모델. At가 정답, Ft가 예측

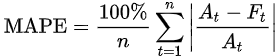
- 5. R-Squared : 분산을 기반으로 한 평가지표. 예측값의 variance / 정답의 variance. 1에 가까울수록 좋은 모델

from sklearn.metrics import r2_score # R-Squared

print(r2_score(valid_t_data, predict_value)) # 0.3734728354920861

 

2. Classification(이항분류)의 Metrics

- Confusion Matrix를 이용해서 Metric을 정의

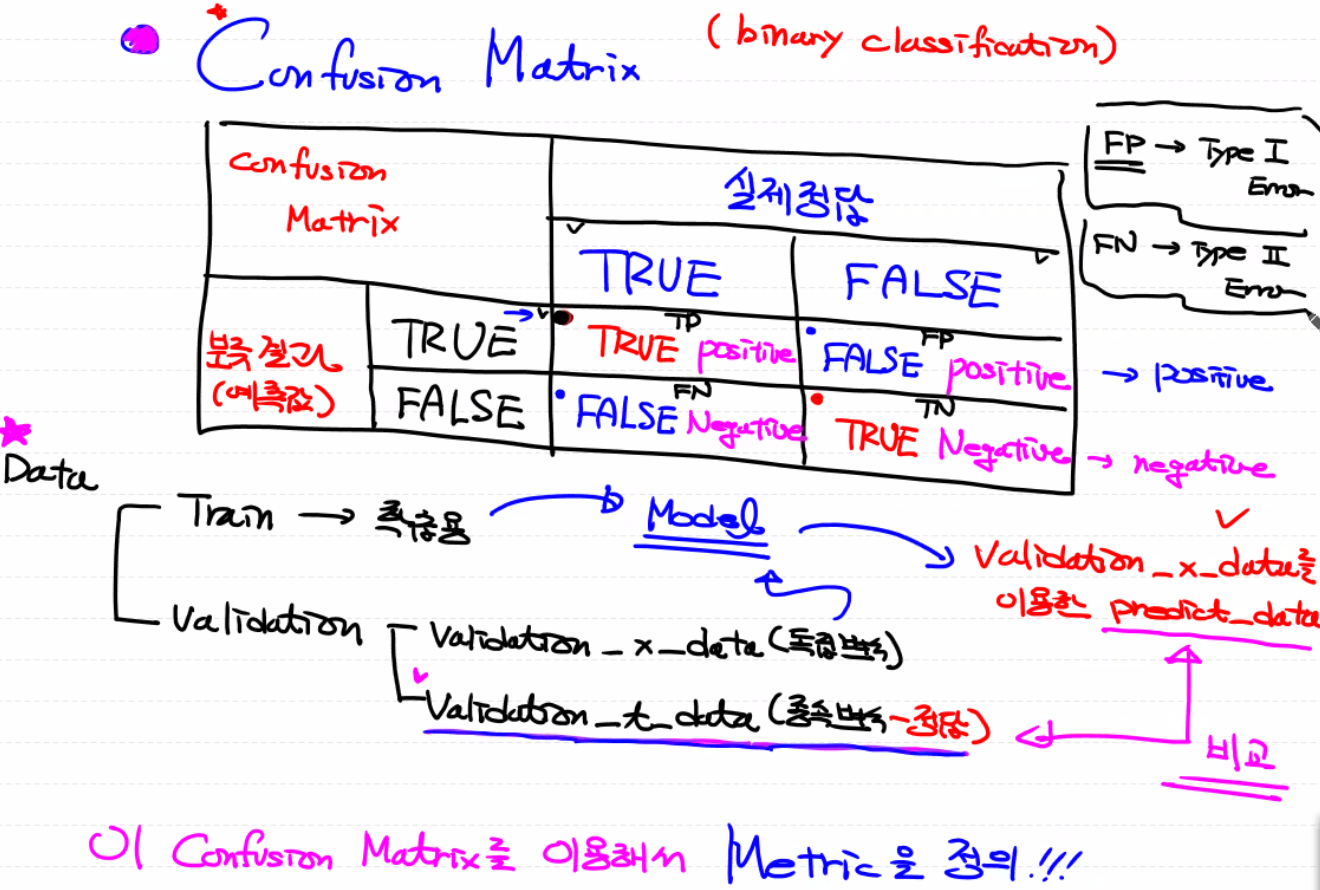
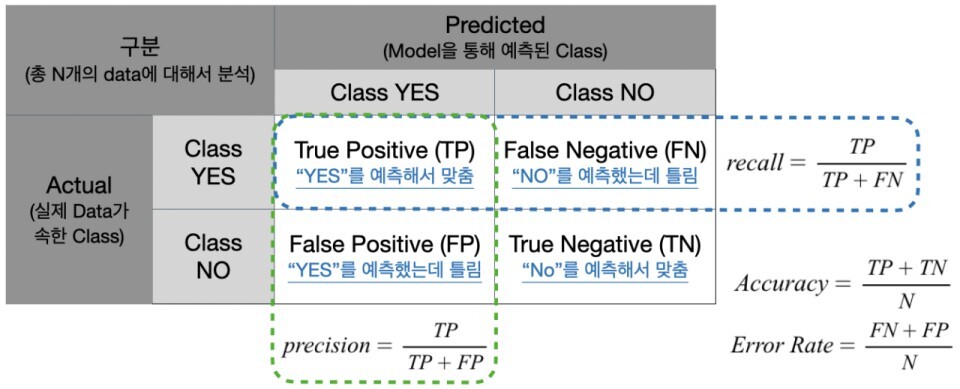
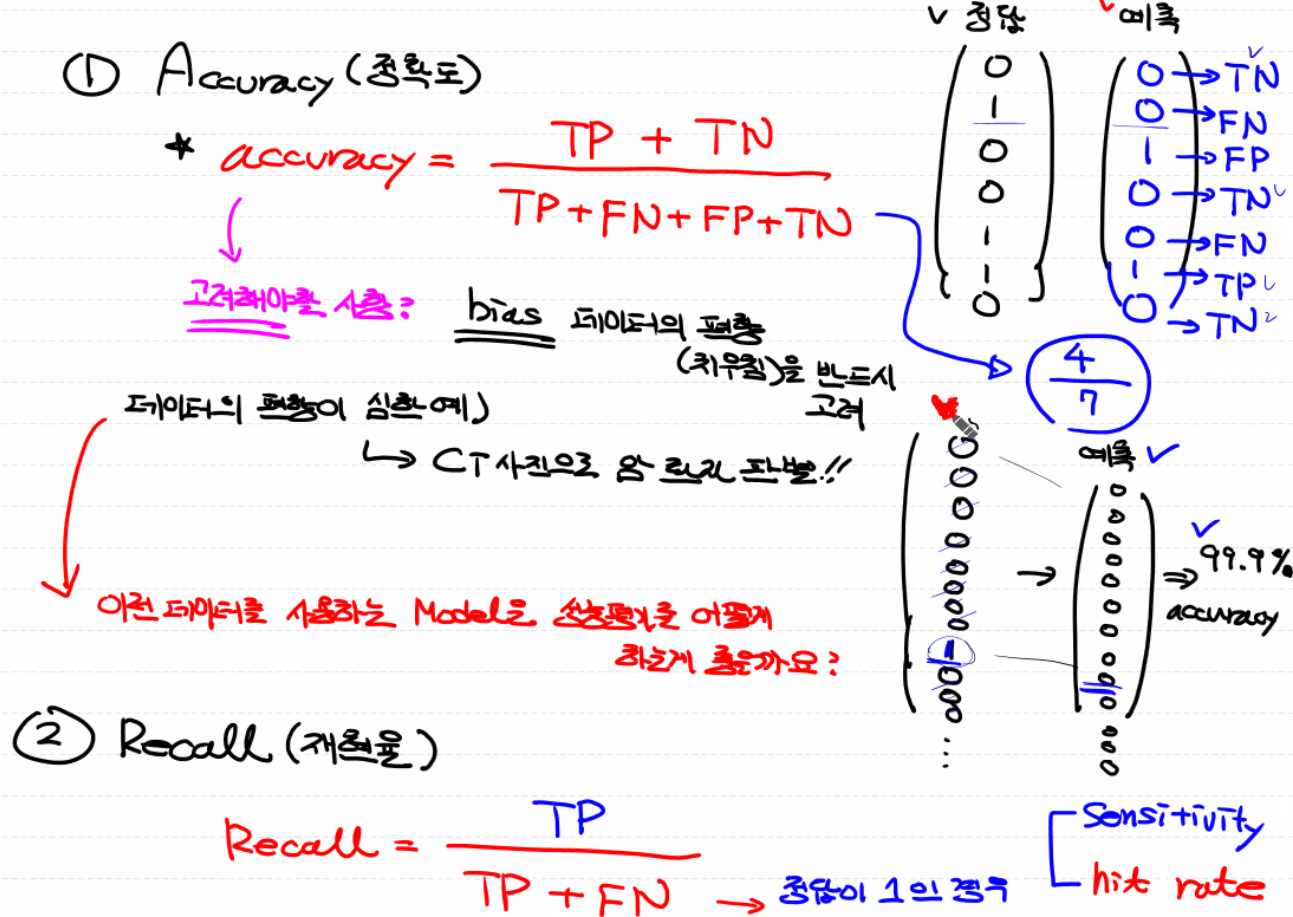
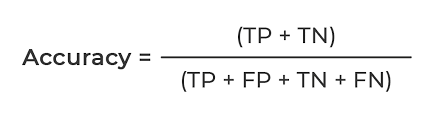
- 1. Accuracy : TP + TN / TP + FN + FP + TN. bias 데이터의 편향(치우침)을 반드시 고려해야 함

- 2. Recall(재현율) : TP / TP + FN. 실제 positive 중에서 얼마나 진짜를 잘 찾았는지에 대한 비율

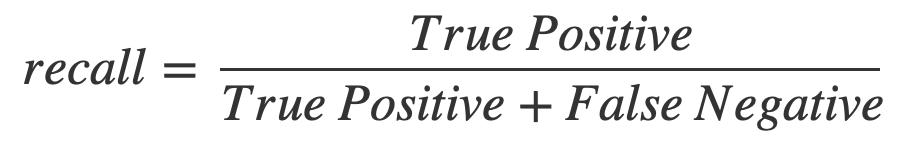
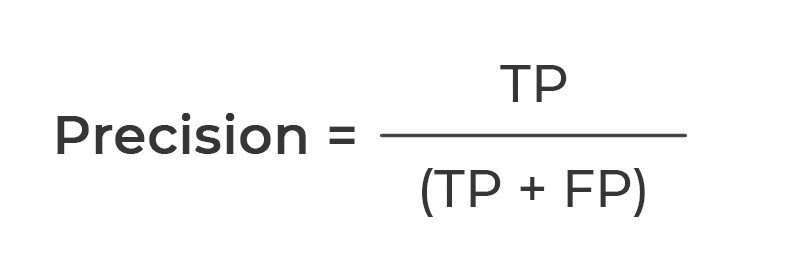
- 3. Precision(정밀도) : TP / TP + FP. positive라고 예측한 것들 중에 얼마나 잘 맞추었는지에 대한 비율. 일반적으로 Recall과 Precision은 반비례 관계. 두 지표 모두 고려해야!

- 4. Precision - Recall graph

 

- 5. F1-Score : Precision과 Recall의 조회 평균

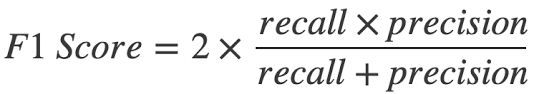
- 6. Fall-out : FP / TN + FP. 실제 값이 False인데 Model이 True로 잘못 예측한 비율

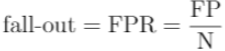
- 7. ROC curve : Recall과 Fall-out의 값을 시각화

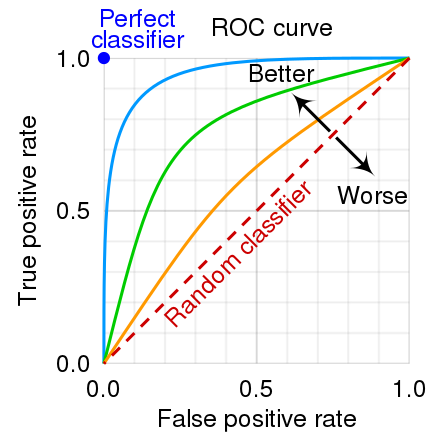
- 8. Log-loss : 다항분류에서 일반적으로 사용

 

1. 3/15 화	2. 3/16 수	3. 3/17 목	4. 3/18 금	5. 3/21 월
ML 환경 설정 (아나콘다, 주피터 노트북), Pandas, Numpy, ndarray	ML Numpy, 행렬곱연산, 전치행렬, iterator, axis, Pandas, Series, DataFrame	ML Pandas, DataFrame, 함수들	ML Pandas, 데이터 분석, 데이터 전처리	ML Pandas, 데이터 전처리, 수행평가
6. 3/22 화	7. 3/23 수	8. 3/24 목	9. 3/25 금	10. 3/28 월
ML 데이터 시각화, Matplotlib, 기술통계	ML 기술통계	ML 기술통계, 머신러닝	ML 미분, Regression	ML 머신러닝 기법들, Regression
11. 3/29 화	12. 3/30 수	13. 3/31 목	14. 4/1 금	15. 4/4 월
ML Regression 구현 (Python, Scikit-Learn)	ML Outlier, Z-score, MinMaxScaler, 다변수	ML Tensorflow, Classification	ML Classification, Logistic Regression	ML 평가지표(Metrics)
16. 4/5 화	17. 4/6 수	18. 4/7 목	19. 4/8 금	20. 4/11 월
ML 평가 시 주의사항

* 열정 열정 열정! 복습 복습 복습!