불금쓰~! 🥳
오늘은 머신러닝에 들어가기에 앞서 수학적인 내용을 배운다!
1. Log : 지수(제곱, 승) 표현에는 익숙함. Log는 지수를 다른 방법으로 표현
Log의 특성을 이용하면, 복잡한 지수방정식을 쉽게 풀 수 있음. 왜? 값을 확 줄여준다! 정규성 ↑
지수방정식은 진수와 분리된 형태, 로그 방정식은 지수가 분리된 형태

Log는 크게 2가지
상용로그(common lodarithm) : 십진로그, 밑이 10
자연로그(natural lodarithm) : 자연로그, 밑이 자연상수 e(2.718...)
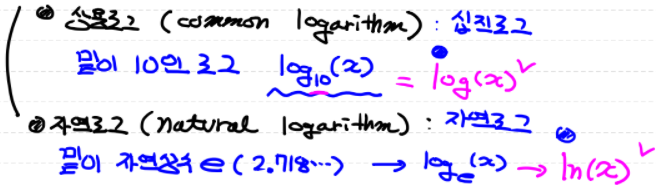
2. 미분 : 어떤 함수의 정의역(두 변수 x, y 사이에 y가 x의 함수로 나타내어질 때에, x가 취할 수 있는 값의 범위) 속 각 점에서 독립변수 값의 변화량과 함수값의 변화량의 비율(직선의 기울기)의 극한, 극한의 집합을 치역(함수가 취하는 값 전체의 집합)으로 가지는 새로운 함수
미분은 함수에 대해서 특정 순간의 변화량(x에서의 작은 변화가 f(x) 함수를 얼마나 변화시키는가)

해석미분 : 종이와 펜을 이용해 논리적인 전개로 수행하는 미분
수치미분 : 해석미분으로 해결할 수 없을 때 수치값을 이용해 미분의 근사값을 얻어내는 방법
수치미분은 전향차분, 후향차분, 중앙차분(가장 값이 정확)이 있음
중앙차분을 구할 때, 델타 x(△x)를 아주 작은 값으로 설정하면 문제가 발생함 → 10의 -4승 정도로 잡음

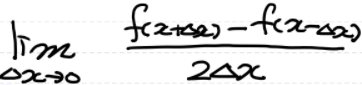
* 미분의 기본 공식들

3. 편미분(partial derivative) : 독립변수 두 개 이상인 다변수 함수에서, 미분하고자 하는 변수 하나를 제외한 나머지 변수를 상수(변수에 대하여 항상 일정한 값을 취하는 양)로 취급해서 해당 변수를 미분하는 방법

4. 미분의 Chain Rule(연쇄 법칙) : 여러 함수로 구성된 합성함수를 미분할 때 사용

5. Python으로 일(단)변수 함수의 수치미분(중앙차분 이용) 코드를 만들고 미분값을 구해보자
def my_func(): # Python의 함수는 변수에 저장되는 개념. 함수 이름이 변수
print('Hello')
my_func() # Hello
print(my_func) # <function my_func at 0x000001BDE34994C0>
# 일급함수(first-classes function)를 지원하는 프로그래밍 언어들(Javascript, Python)이 있음. C 언어는 일급함수를 지원하지 않음
# 함수 이름이 변수 이름이기 때문에, 변수(다른 함수의 인자로)처럼 사용할 수 있음
def my_func2(x): # 파라미터로 변수를 넘김
print(x + 10)
tmp = 20
my_func2(tmp) # 30
def my_func3(x):
x(20)
def my_func4(x):
print(x + 30)
my_func3(my_func4) # 50# f(x) = x^2 # 미분값을 구하는 함수를 만들어 보자
# f'(x) = 2x
# f'(5) = 10 # 해석미분
def my_func(x): # 우리가 가지고 있는 함수 f(x)
return x ** 2
def numerical_derivative(f,x): # 미분을 수행하는 함수
delta_x = 1e-4 # 극한에 해당하는 값. 너무 작은 값을 사용하면 실수 계산 오류 발생
# 1e-4 정도의 값을 이용하면, 적당한 수치미분 값(근사값)을 구할 수 있음
return (f(x + delta_x) - f(x - delta_x)) / (2 * delta_x)
# f'(5)
result = numerical_derivative(my_func, 5)
print(result) # 9.999999999976694
6. Python으로 다변수 함수의 수치미분(중앙차분 이용) 코드를 만들고 미분값을 구해보자
# Python으로 다변수 함수의 수치미분(중앙차분 이용) 코드를 만들고 미분값을 구해보자
# f(x,y) = 2x + 3xy + y^3 # 2변수 함수
# f'(1.0, 2.0) = ??
# f(a, b, c) = 3a + 3bc + b^2 + c^3 # 3변수 함수
import numpy as np
# def my_func(x,y): # 이렇게 구현하면, 다변수 함수의 수치미분 코드를 3변수 이상에 대해서 각각 구현해야함
# return 2 * x + 3 * x * y + y ** 3
# print(my_func(1.0, 2.0)) # 16.0
def my_func(input_value): # input_value = [x,y] 리스트로 값이 2개 넘어온다. ndarray로 들어올 경우 [x y]
x = input_value[0]
y = input_value[1]
return 2 * x + 3 * x * y + y ** 3
# x : [1.0, 2.0] → 결과 : [8.0, 15.0] / x : [1.0, 2.0, 3.0] → 결과 : [8.0, 15.0, 20]
def numerical_derivative(f,x): # 다변수 함수의 수치미분 코드. input_value = [x y] ndarray로 값이 2개 넘어온다
# x : [[1.0 2.0]
# [3.0 4.0]]
# → 결과 : [[8.0 15.0]
# [20.0 30.0]]
delta_x = 1e-4
derivative_x = np.zeros_like(x) # derivative_x : [0.0 0.0]. x의 shape과 같도록 ndarray 만듦
# iterator를 이용해서 입력변수 x에 대한 편미분을 수행
it = np.nditer(x, flags=['multi_index']) # iterator 객체를 얻어 변수 넣고 flags라는 속성으로 차원 정해주고 반복~
while not it.finished:
idx = it.multi_index
tmp = x[idx] # tmp : 1.0
x[idx] = tmp + delta_x # x : ndarray [1.0001 2.0]
fx_plus_delta = f(x)
x[idx] = tmp - delta_x # x : ndarray [0.9999 2.0]
fx_minus_delta = f(x)
derivative_x[idx] = (fx_plus_delta - fx_minus_delta) / (2 * delta_x)
x[idx] = tmp # x : ndarray [1.0 2.0]
it.iternext()
return derivative_x
result = numerical_derivative(my_func, np.array([1.0, 2.0]))
print(result) # [ 8. 15.00000001]# Python으로 4변수 함수의 수치미분(중앙차분 이용) 코드를 만들고 미분값을 구해보자
# f(w,x,y,z) = wx + xyz + 3w + zy^2
# 수치미분
# f'(1.0, 2.0, 3.0, 4.0) = ?
def my_func(input_value): # [[1.0 2.0
# 3.0 4.0]]
w = input_value[0,0]
x = input_value[0,1]
y = input_value[1,0]
z = input_value[1,1]
return (w*x) + (x*y*z) + (3*w) + (z*(y**2))
result = numerical_derivative(my_func, np.array([[1.0, 2.0], [3.0, 4.0]]))
print(result)
# [[ 5. 13.]
# [32. 15.]]미분 내용 끝!
머신러닝 시작!
1. Regression(회귀) : 데이터에 영향을 주는 조건들의 영향력을 고려해서, 데이터에 대한 조건부 평균을 구하는 기법

| 1. 3/15 화 | 2. 3/16 수 | 3. 3/17 목 | 4. 3/18 금 | 5. 3/21 월 |
| ML 환경 설정 (아나콘다, 주피터 노트북), Pandas, Numpy, ndarray |
ML Numpy, 행렬곱연산, 전치행렬, iterator, axis, Pandas, Series, DataFrame |
ML Pandas, DataFrame, 함수들 |
ML Pandas, 데이터 분석, 데이터 전처리 |
ML Pandas, 데이터 전처리, 수행평가 |
| 6. 3/22 화 | 7. 3/23 수 | 8. 3/24 목 | 9. 3/25 금 | 10. 3/28 월 |
| ML 데이터 시각화, Matplotlib, 기술통계 |
ML 기술통계 |
ML 기술통계, 머신러닝 |
ML 미분, Regression |
ML |
* 미분 빠개자!!



