수요일!
오늘은 기술통계를 배운다.
1차원 데이터의 특징 파악
- 수치지표 → 대표값 : 평균, 중위값, 최대/최소값, 편차, 분산, 표준편차...
- 시작적 표현 → 도수분포표, Histogram, Box plot
* 최대/최소값은 대표값으로 사용하기에 무리가 있음
2차원 데이터의 특징 파악
- 수치지표 → 공분산, 상관계수
- 시작적 표현 → Scatter
산포도(dispersion) : 데이터가 얼마나, 어떻게 퍼져 있나가 관점
데이터가 흩어진 정도(변산성)를 수치로 표현하고 싶다면 → 범위(range), 사분위 범위(IQR, Interquatile range), 편차(deviation), 분산(variance), 표준편차(standard deviation)
1차원 데이터의 수치지표 → 평균, 중위값, 최빈값, 편차, 분산, 표준편차, 범위, 사분위
1. 평균(mean) : 이상치(outlier) 때문에 대표값으로 사용하기가 곤란 → 절사평균(Trimmed mean, 최소/대값 제외)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('./data/student_scores_em.csv',
index_col='student number')
# print(df.shape)
# display(df.head(3))
scores = df['english'][:10] # 영어 성적 상단 10개만 슬라이싱
scores_df = pd.DataFrame(scores)
# display(scores_df)
print(scores.mean()) # 55.0. Series의 메서드
print(np.mean(scores)) # 55.0. Numpy의 함수
print(scores_df.mean()) # 55.0. Pandas(DataFrame)의 메서드. 결과는 Series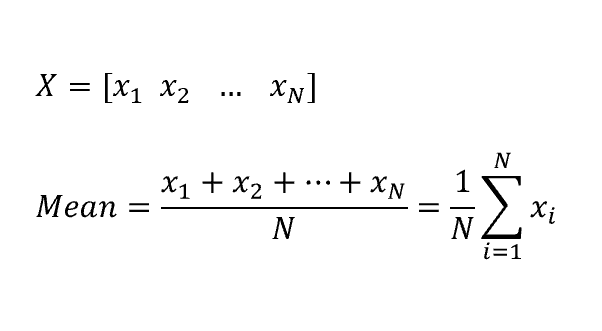
2. 중위값(median) : 전 범위 중 딱 중간에 있는 값. 요소 개수가 짝수일 경우 중간값 두 개의 평균으로 계산
print(np.median(scores)) # 56.5. Numpy의 함수. 중위값
3. 최빈값(mode) : 가장 많이 등장한 값, 빈도. Numpy는 함수 없지만 Pandas는 있음
print(pd.Series([1,1,1,2,2,3]).mode()) # 1. Pandas의 함수. 최빈값
4. 편차(deviation) : 각 데이터가 평균으로부터 얼마나 떨어져 있나 → 값이 여러 개라 활용하기 어려움, 대신 분산을 이용
deviation = scores - np.mean(scores) # 편차. Series - Scala(broadcasting). 값이 여러개라 활용하기 어려움
print(deviation)
print(deviation.mean()) # 0. 편차의 평균(합)
# student number
# 1 -13.0
# 2 14.0
# 3 1.0
# 4 -14.0
# 5 2.0
# 6 -7.0
# 7 10.0
# 8 -6.0
# 9 10.0
# 10 3.0
# Name: english, dtype: float64
5. 분산(variance) : 데이터가 흩어진 정도를 숫자로 표현. 편차의 제곱의 합을 전체 변량의 수로 나눔(편차의 제곱의 평균)
하지만 제곱 때문에 실제 변산성보다 더 큰 값을 가짐 → 분산의 제곱근을 구해서(루트) 원래 단위로 돌리기, 표준편차
print(np.mean(deviation ** 2)) # 86.0. 분산, 편차의 제곱의 평균
print(np.var(deviation)) # 86.0. Numpy의 함수. 분산
print(scores_df.var()) # 95.555556. Pandas(DataFrame)의 메서드. 모든 컬럼에 대한 분산을 구함
# 왜 Numpy / Pandas의 분산 값이 다를까?
# 표본분산 : Numpy, 통상적
# 불편분산 : Pandas, 편차의 제곱의 합을 n으로 나누는 것이 아닌 n-1로 나눔. 분모가 작아서 값이 커짐!
print(scores_df.var(ddof=0)) # 86.0. ddof=0 옵션을 줘서 표본분산을 구함. ddof=1은 불편분산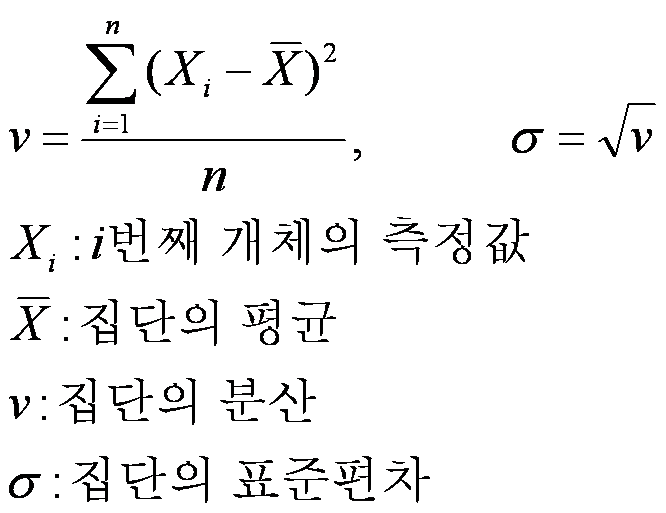
6. 표준편차(standard deviation) : 분산의 제곱근을 구해서(루트) 변산성을 원래 단위로 돌림
print(np.sqrt(np.var(scores))) # 9.273618495495704. Numpy의 함수. 표준편차. 분산에 루트를 씌워서 제곱근을 구하라
print(np.std(scores)) # 9.273618495495704. Numpy의 함수. 표준편차. Series의 표준편차를 구하라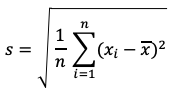
7. 범위(range) : 최대값 - 최소값. 범위 값이 크면 산포도가 큼, 작으면 산포도가 작음. 이상치에 아주 민감함
8. 사분위 범위(IQR, Interquatile range) : 데이터의 1사분위(Q1, 하위 25%), 2사분위(Q2, 50%), 3사분위(Q3, 75%)를 찾아 Q3 - Q1을 구함
Q1 = np.percentile(scores, 25) # Numpy의 함수. 1사분위(Q1, 25%)
Q2 = np.percentile(scores, 50) # 2사분위(Q2, 50%) = 중위값(median)
Q3 = np.percentile(scores, 75) # 3사분위(Q3, 75%)
IQR = Q3 - Q1
print(IQR) # 15.0. 사분위 범위(IQR)
9. 1차원 데이터의 시작적 표현 → 도수분포표, Histogram, Box plot
데이터의 분포 상태를 도표로 확인 : 데이터가 취하는 값을 몇 개의 구간(class, 계급)으로 나누고, 각 구간에 몇 개의 데이터가 들어가 있는지(frequency, 도수), 구간의 폭(class interval, 계급의 크기), 계급수(class의 개수)을 구함 → 도수분포표(Frequency Distribution Table)
df = pd.read_csv('./data/student_scores_em.csv',
index_col='student number')
scores = df['english'].values # 영어성적을 가지고 ndarray 생성
print(scores)
freq, tmp = np.histogram(scores, bins=10, range=(0, 100)) # 경계값과 데이터 범위를 지정
print(tmp) # 경계값 구함
print(freq) # 각 구간에 몇 개의 데이터가 들어가 있는지(frequency, 도수)
# 단변수(1차원) 데이터의 도수분포표를 DataFrame으로 만들기
freq_class = [str(i) + '~' + str(i+10) for i in range(0, 100, 10)] # 행 index부터 만들기(list comprehension)
print(freq_class)
freq_dist_df = pd.DataFrame({'Frequency':freq}, index=freq_class)
display(freq_dist_df)
10. 도수분포표(Frequency Distribution Table) : → class(계급), frequency(도수)
- class mark(계급값) : 중위값(median)을 이용해 class(구간)를 값으로 표현
- relative frequensy(상대도수) : 전체 데이터에 대해 해당 class의 도수가 얼마 만큼의 비율을 차지하고 있는지
- cumulative relative frequency(누적 상대도수) : 해당 class까지 상대도수의 누적
df = pd.read_csv('./data/student_scores_em.csv',
index_col='student number')
scores = df['english'].values
# print(scores)
freq, tmp = np.histogram(scores, bins=10, range=(0, 100))
# 도수분포표
freq_class = [str(i) + '~' + str(i+10) for i in range(0, 100, 10)]
freq_dist_df = pd.DataFrame({'Frequency':freq}, index=freq_class)
# class mark(계급값). class(구간)를 값으로 표현
class_mark = [(i + (i+10)) / 2 for i in range(0,100,10)]
freq_dist_df['class_mark'] = class_mark
# relative frequensy(상대도수). 전체 데이터에 대해 해당 class의 도수가 얼마 만큼의 비율을 차지하고 있는지
rel_freq = freq / freq.sum()
freq_dist_df['rel_freq'] = rel_freq
# cumulative relative frequency(누적 상대도수). 해당 class까지 상대도수의 누적
# print(rel_freq)
# print(np.cumsum(rel_freq)) # Numpy의 함수. 누적 상대도수
freq_dist_df['cum_rel_freq'] = np.cumsum(rel_freq)
display(freq_dist_df)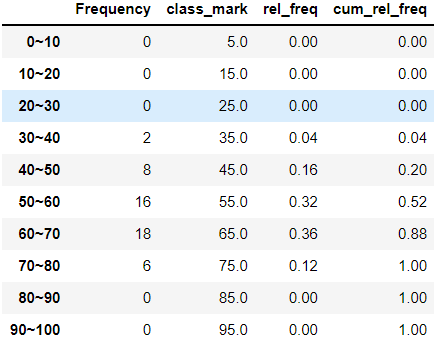
11. Histogram
import matplotlib.pyplot as plt
df = pd.read_csv('./data/student_scores_em.csv',
index_col='student number')
scores = df['english'].values
figure = plt.figure(figsize=(10,6))
ax = figure.add_subplot(1,1,1)
ax.hist(scores, bins=10, range=(1,100))
plt.show()
12. Box plot. 사분위 범위(IQR, Interquatile range)
최대값 : 이상치의 경계가 되는 최대값 = Q3 + (IQR * 1.5)
최소값 : 이상치의 경계가 되는 최소값 = Q1 - (IQR * 1.5)
import matplotlib.pyplot as plt
df = pd.read_csv('./data/student_scores_em.csv',
index_col='student number')
scores = df['english'].values
fig = plt.figure(figsize=(10,6))
ax = fig.add_subplot(1,1,1)
ax.boxplot(scores)
plt.show()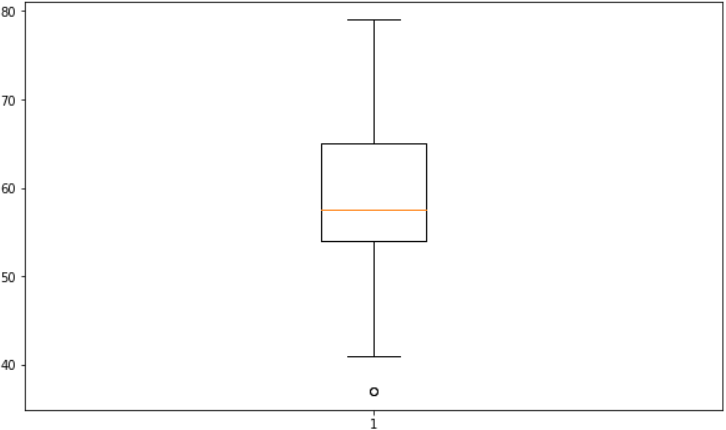
2차원 데이터의 수치지표 → 공분산, 상관계수
13. 공분산(covariance) : 두 확률변수 사이의 상관 정도

| 1. 3/15 화 | 2. 3/16 수 | 3. 3/17 목 | 4. 3/18 금 | 5. 3/21 월 |
| ML 환경 설정 (아나콘다, 주피터 노트북), Pandas, Numpy, ndarray |
ML Numpy, 행렬곱연산, 전치행렬, iterator, axis, Pandas, Series, DataFrame |
ML Pandas, DataFrame, 함수들 |
ML Pandas, 데이터 분석, 데이터 전처리 |
ML Pandas, 데이터 전처리, 수행평가 |
| 6. 3/22 화 | 7. 3/23 수 | 8. 3/24 목 | 9. 3/25 금 | 10. 3/28 월 |
| ML 데이터 시각화, Matplotlib, 기술통계 |
ML 기술통계 |
ML 기술통계 |
ML |
ML |
* 용어 난무!



